Invers Matriks: Cara Praktis Mencari dengan Langkah Mudah
Invers Matriks: Cara Praktis Mencari dengan Langkah Mudah
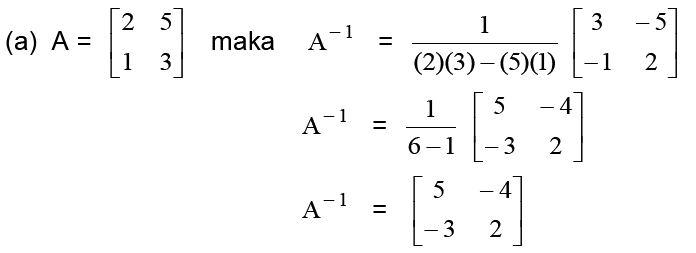
Gambar ini menjelaskan cara mudah dan terbaru untuk mencari invers matriks 3x3. Prosesnya dimulai dengan menulis matriks awal, kemudian dilakukan operasi- operasi sederhana untuk memperoleh matriks inversnya. Dengan bantuan rumus dan langkah-langkah yang jelas, kita dapat dengan mudah mencari invers matriks dengan akurasi tinggi dan waktu yang efisien.
Berbicara tentang matriks, mungkin sebagian besar dari kita sudah tidak asing lagi. Matriks adalah suatu array dari bilangan-bilangan atau variabel-variabel yang diatur dalam bentuk baris dan kolom. Matriks juga memiliki beragam operasi yang bisa dilakukan, salah satunya adalah mencari invers matriks.
Mencari invers matriks merupakan langkah yang penting dalam matematika, terutama dalam kalkulus dan pengolahan data. Invers matriks digunakan untuk menyelesaikan berbagai masalah, misalnya untuk menyelesaikan sistem persamaan linear, melakukan transformasi geometri, dan banyak lagi.
Apakah Anda ingin tahu bagaimana cara mencari invers matriks dengan mudah dan praktis? Simak penjelasan berikut ini!
Apa Itu Invers Matriks?
Sebelum masuk ke metode mencari invers matriks, ada baiknya kita memahami terlebih dahulu apa yang dimaksud dengan invers matriks.
Invers matriks dari suatu matriks persegi A dinyatakan sebagai A-1 dan memenuhi persamaan A * A-1 = A-1 * A = I, di mana I adalah matriks identitas. Artinya, ketika matriks A dikalikan dengan inversnya, hasilnya akan selalu menjadi matriks identitas.
Secara geometri, invers matriks berfungsi seperti kebalikan dari matriks yang diberikan. Jika kita melihat matriks sebagai transformasi geometri, invers matriks akan membatalkan transformasi tersebut sehingga membawa kita kembali ke titik awal. Contohnya, jika sebuah matriks digunakan untuk memutar sebuah objek, invers matriks akan digunakan untuk memutar objek tersebut ke posisi semula.
Mencari Invers Matriks dengan Metode Adjoin
Terdapat beberapa metode yang bisa digunakan untuk mencari invers matriks, salah satunya adalah metode adjoin. Metode ini cukup praktis dan mudah untuk diterapkan. Berikut ini adalah langkah-langkahnya:
Langkah 1: Periksa Determinan Matriks
Langkah pertama dalam mencari invers matriks adalah memeriksa apakah matriks tersebut memiliki determinan yang tidak sama dengan nol. Jika determinan matriks A adalah nol, maka matriks tidak memiliki invers. Dalam hal ini, pencarian invers matriks berhenti dan tidak mungkin dilanjutkan.
Langkah 2: Membuat Matriks Adjoin
Jika matriks A memiliki determinan yang tidak sama dengan nol, langkah selanjutnya adalah membuat matriks adjoin. Matriks adjoin diperoleh dengan menukar elemen-elemen diagonal utama dengan elemen-elemen diagonal kedua matriks kofaktor yang berlawanan tanda.
Langkah 3: Mencari Invers Matriks
Setelah mendapatkan matriks adjoin, kita dapat mencari invers matriks dengan rumus berikut:
A-1 = (1/det(A)) * adj(A)
Dalam rumus di atas, det(A) adalah determinan matriks A, dan adj(A) adalah matriks adjoin yang telah ditemukan pada langkah sebelumnya.
Contoh Mencari Invers Matriks
Untuk memahami lebih lanjut tentang cara mencari invers matriks menggunakan metode adjoin, berikut ini adalah contoh perhitungan:
Misalkan kita memiliki matriks A berikut:
[1 2]
[3 4]
Langkah pertama adalah memeriksa determinan matriks A.
det(A) = (1 * 4) - (2 * 3) = 4 - 6 = -2
Karena determinan matriks A tidak sama dengan nol, kita dapat melanjutkan dengan langkah berikutnya.
Langkah kedua adalah membuat matriks adjoin. Dalam contoh ini, matriks adjoin A diperoleh dengan menukar elemen diagonal utama dengan elemen diagonal kedua matriks kofaktor yang berlawanan tanda, sehingga:
adj(A) = [4 -3]
[-2 1]
Langkah terakhir adalah mencari invers matriks A menggunakan rumus:
A-1 = (1/-2) * [4 -3]
[-2 1]
Setelah melakukan perhitungan, didapatkan:
A-1 = [-2 3/2]
[1 -1/2]
Kesimpulan
Mencari invers matriks memang bisa menjadi proses yang rumit jika tidak tahu langkah-langkah yang tepat. Namun, dengan metode adjoin, kita bisa mencari invers matriks dengan mudah dan praktis.
Dalam mencari invers matriks, langkah pertama yang perlu dilakukan adalah memeriksa determinan matriks. Jika determinan matriks tidak sama dengan nol, kita dapat melanjutkan dengan membuat matriks adjoin. Selanjutnya, kita bisa mencari invers matriks dengan rumus A-1 = (1/det(A)) * adj(A).
Metode adjoin ini cukup sederhana dan bisa dilakukan secara manual atau menggunakan perangkat lunak matematika. Dengan memahami langkah-langkah yang tepat, kita dapat mencari invers matriks dengan mudah dan mendapatkan hasil yang akurat.
Jadi, ketika Anda ingin mencari invers matriks dalam perhitungan atau masalah matematika lainnya, jangan ragu untuk menggunakan langkah-langkah di atas. Invers matriks akan memberikan solusi yang akurat dalam berbagai aplikasi matematika yang melibatkan matriks.
Dengan begitu, Anda dapat melakukan transformasi atau perhitungan lainnya dengan lebih efisien dan efektif. Jadi, buatlah sekarang juga langkah-langkah pencarian invers matriks menjadi rutinitas dalam matematika Anda!